支持向量机的原理及python实现

概述

  支持向量机(support vector machine，一般称为SVM。是一种二类分类模型，其基本模型定义为特征空间上的间隔最大的线性分类器，其学习策略便是间隔最大化，最终可转化为一个凸二次规划问题的求解。
  因为其较低的错误率，使其被认为是机器学习中目前为止最好的分类器。

基本概念

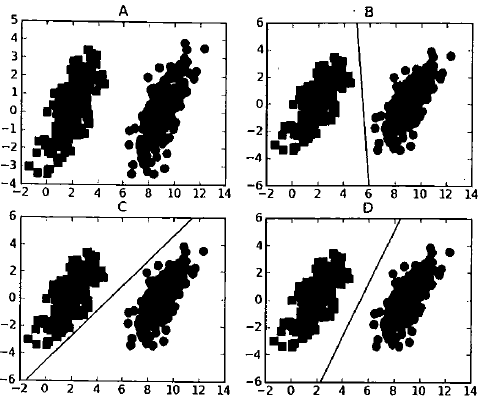
  上图一共有四个部分，A为原始数据集，一共有两类，分别在左边和右边，B，C，D分别给出了一条可以将两类分开的直线。这条直线被称为分隔超平面。如果是在二维平面上，这个超平面就是一条直线，如果是三维的，就是一个平面。如果数据集是N维的话，就需要一个N-1维的对其分隔，也就是分类的决策边界。
  对于上图的三种决策边界，我们明显认为D的决策边界是最好的，因为其距离两类的间距都是最大的。也就是说，我们希望找到离分隔超平面最近的点，确保它们离分隔面的距离尽可能地远。这里点到分割面地距离被称为间隔。我们希望间隔尽可能地大。
  而所谓的支持向量就是离分隔超平面最近的那些点，机的意思就是决策边界。所以接下来的任务就是最大化支持向量到分隔面的距离。

任务——寻找最大间隔

  首先我们要确定点到决策边界的距离，也就是所谓的函数间隔(可能有的书这里指的是几何间隔)。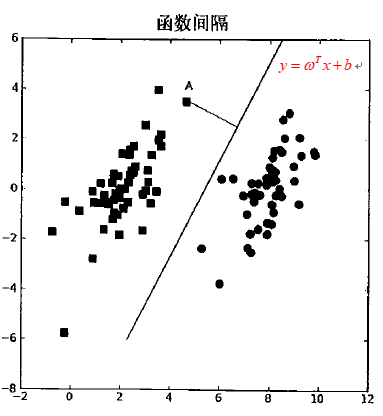

  分隔超平面的直线可以记为$y=\omega ^Tx + b$(这里的$\omega$和$x$都是一个向量，$b$类似于截距)，然后计算点A到分隔面的法线或垂线的长度，利用点到平面的公式可以得到其函数间隔为：

$$d=\frac{\left | \omega ^{T}x+b \right |}{\left \| \omega \right \|}$$

  所以我们对一个数据点进行分类时，当超平面离数据点的“间隔”越大，分类的置信度也越大。为了使得分类的确信度尽量高，需要让所选择的超平面能够最大化这个“间隔”值。
  但是只有这个间隔也不够，因为我们有两类数据，所以还需要再定义类别标签的概念。
  这里的类别的定义和之前的机器学习算法不同，使用的是-1和+1两种标签，即：

$$g\left ( z \right )=g\left ( \omega ^{T}x+b \right )=\left\{\begin{matrix} -1 & z\geqslant 0\\ 1 & z < 0 \end{matrix}\right.$$

  为什么这样定义呢？因为之前我们定义的间隔公式中含有绝对值项$\left | \omega ^{T}x+b \right |$，这对后面的计算来说不太方便，而现在我们可以将其替换为$lable\left ( \omega ^{T}x+b \right )$，因为这是一个恒正的表达式。如果数据点处于正方向(+1类)，并且离分隔面很远的位置时，$\left ( \omega ^{T}x+b \right )$会是一个很大的正数，同时$lable\left ( \omega ^{T}x+b \right )$也是一个很大的正数。反之，如果在负方向，其最终的值也是一个正数(负负得正)。而且标签值为+1和-1，也不影响最终的间距值。
  综上所述，我们最终的目标任务可以用以下的数学表达式表示：

$$arg \underset{\omega,b}{max}\left \{ \underset{n}{min}\left ( label\cdot \left ( \omega ^{T}x+b \right ) \right ) \cdot \frac{1}{\left \| \omega \right \|}\right \}$$

  公式前面的$argmax$表示的是间隔最大值时，参数$\omega,b$的取值。$min$表示的是具有最小间隔的数据点。
  但是这里面都是乘积项，对其求最值比较困难，如果能固定某个乘积项，只求其中一个的最值就会简单很多，而经过之前的分析，$lable*\left ( \omega ^{T}x+b \right )$项都是大于0的，在准确地说其值是$\geqslant 1$的(如下图所示)。那么其最小值为1，就可以去掉该项。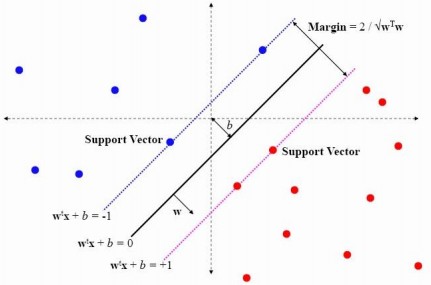

  所以我们就将此问题转换为了约束条件下的极值问题，即
  目标函数为：

$$max\frac{1}{\left \| \omega \right \|}$$

  约束条件为：

$$s.t. \quad \quad y_i*\left ( \omega ^{T}x_i+b \right) \geqslant 1,i=1,2,...,n$$

注：这里的$label$替换为了$y_i$。