贝叶斯算法

发表于 | 更新于 | 分类于 | 评论数： | 阅读次数：
本文字数： 2,857字 | 阅读时长 ≈ 11 分钟

贝叶斯算法

一、基本原理

  贝叶斯算法属于有监督的学习算法，即原始数据集是已知的，其主要思想为根据在一定特征下属于哪个类别的条件概率大小来判断分类。
  条件概率是指事件A在另外一个事件B已经发生条件下的发生概率,记为P(A|B),B为条件，A为需要计算的概率。其计算公式为：P(A|B)=P(AB)/P(B),但一般来说A,B事件不是独立事件，即P(AB)不等于P(A)P(B)，所以一般用贝叶斯公式将其展开，即：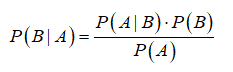
条件概率公式
  对应于分类算法的意义，该公式可以表示为：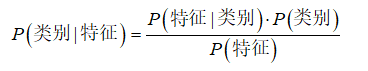
贝叶斯算法条件概率公式_文字
  P(类别|特征)：在一定特征下属于该类别的概率，即我们最终用来判断分类的概率。P(特征|类别)：在该类别下的特征概率。即在已知类别的情况下，每个特征出现的频数除以总的特征数。P(类别)：数据集中的每个类别的概率，即每个类别的次数除以数据集的总个数。P(特征)：特征的概率，由于数据集是一样的，其特征也一样，计算概率时，可忽略该项。
  哪个分类的条件概率大就判定为哪个类别，这也是贝叶斯算法的核心思想。其计算公式中最重要的部分就是每个特征的在对应类别下的概率。有多少个特征就要进行多少次计算，这里我们假设每个特征都是相互独立的，即任意2个特征都不相互影响分类结果，这也称为朴素贝叶斯算法。

二、算法实现（文本分类）

  对一个在线社区的留言板内容构建一个过滤器，如果某条留言使用了负面的语言，则将该留言标识为内容不当。
  首先需要将文本转换为数字向量以便为标识，然后基于这些向量来计算条件概率(贝叶斯算法)并在此基础上构建分类器。

准备数据

  首先将获得的每句话的文本数据存在于列表中，然后将所有的文本数据整合到一个列表中，此时列表中的所有单词元素应该是唯一的。最后创建一个文档向量，向量的每一个元素为1或0，分别表示词汇表中的单词在输入单词列表中是否存在。
  此时单词列表中的单词就是数据集的特征，即1个单词对应1个特征。
程序实现：

1
2
3
4
5
6
7
8
9
def loadDataSet():
    postingList = [['my', 'dog', 'has', 'flea', 'problems', 'help', 'please'],
                   ['maybe', 'not', 'take', 'him', 'to', 'dog', 'park', 'stupid'],
                   ['my', 'dalmation', 'is', 'so', 'cute', 'I', 'love', 'him'],
                   ['stop', 'posting', 'stupid', 'worthless', 'garbage'],
                   ['mr', 'licks', 'ate', 'my', 'steak', 'how', 'to', 'stop', 'him'],
                   ['quit', 'buying', 'worthless', 'dog', 'food', 'stupid']]
    classVec = [0, 1, 0, 1, 0, 1]
    return postingList, classVec

程序说明：
  postingList为文本数据。首先将每句话存放在一个列表中，然后将每个单词用逗号隔开。classVec为已知的分类标签，即事先对每句话划分好的标签。0表示这句话是正面的，1表示负面的。 

1
2
3
4
5
6
def createVocabList(dataSet):
    vocabSet = set([])
    # 遍历输入数据集中的每一句话
    for document in dataSet:
        vocabSet = vocabSet | set(document)
    return list(vocabSet)

  createVocabList()函数生成一个包含所有数据集的单词列表，且列表中的单词都是唯一的。
  首先创建一个空列表，set()函数保证了其唯一性，然后分别将此与数据集中每一句的单词列表进行’与’操作，即将数据集的每句话中不重复的单词添加到空列表中。

1
2
3
4
5
6
7
8
9
def setOfWords2Vec(vocabList, inputSet):
    returnVec = [0] * len(vocabList)
    for word in inputSet:
        # 如果输入数据集中的单词在单词列表中则记为1
        if word in vocabList:
            returnVec[vocabList.index(word)] = 1
        else:
            print("the word: %s is not in my Vocabulary!" % word)
    return returnVec

  setOfWords2Vec()创建一个文档向量。该函数对输入的数据中的每个单词进行搜索，如果该单词在单词列表中，则记为1。

1
2
3
4
listOPosts, listClasses = loadDataSet()
myVocabList = createVocabList(listOPosts)
returnVec_0 = setOfWords2Vec(myVocabList, listOPosts[0])
returnVec_1 = setOfWords2Vec(myVocabList, listOPosts[1])

程序输出为：

1
2
3
['to', 'how', 'dog', 'ate', 'park', 'is', 'food', 'my', 'steak', 'flea', 'take', 'problems', 'buying', 'I', 'mr', 'love', 'posting', 'not', 'garbage', 'maybe', 'licks', 'dalmation', 'cute', 'please', 'quit', 'stop', 'help', 'him', 'stupid', 'so', 'worthless', 'has']
[0, 0, 1, 0, 0, 0, 0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 1]
[1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0, 0]

  myVocabList就是单词列表，也就是该数据集的所有特征。第1个文档向量的输入数据为第1句话，第1个元素’0’表示’to’这个单词没有在第1句话出现，第2个文档向量的输入数据为第2句话，第1个元素’1’表示’to’这个单词在第2句话中有出现。
  一共有6组数据列表，每个列表的长度即单词列表的长度，即不重复单词的个数，也就是数据集的特征总数。

训练算法

  得到数据集的每组特征后，便可以利用贝叶斯的条件概率公式训练算法。其计算公式可以改写为：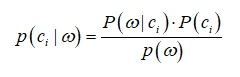
贝叶斯算法条件概率公式
  w表示特征，c表示分类。对每个类别都进行计算，最后比较对应的概率值大小就可以判断其分类。
  p(c)表示类别出现的概率，即在原始数据集中每个类型出现的概率。例如在数据集的6句话中，负面评论共3次，则类别0的概率为3/6=0.5。
  p(w|c)表示在该类别下该特征的频率。即在已知类别的情况下，每个特征出现的概率。由于原始数据集不仅只有1个特征，所以需要对每个特征进行计算并求积。即：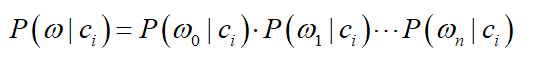
特征计算公式
  每个特征的概率计算方法为：每个特征在某个类别下出现的次数/该类别下的总特征数。
程序实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
def trainNBO(trainMatrix, trainCategory):
    numTrainDocs = len(trainMatrix)  # 输入文档的长度，即共有几组数据
    numWords = len(trainMatrix[0])   # 单词的个数，即每组数据有多少个单词
    pAbusive = sum(trainCategory) / float(numTrainDocs)  # 是负面标签的概率 
    p0Num = ones(numWords)
    p1Num = ones(numWords)
    p0Denom = 0.0
    p1Denom = 0.0
    for i in range(numTrainDocs):
        if trainCategory[i] == 1:
            # 计算当类别标签为1时，各个单词出现的次数
            p1Num += trainMatrix[i]  # 标签为1的类别下，每个单词出现的次数+1
            p1Denom += sum(trainMatrix[i])  # 标签为1的类别下，单词在单词表中出现的总次数
        else:
            p0Num += trainMatrix[i]		
            p0Denom += sum(trainMatrix[i])
    p1Vect = p1Num / p1Denom
    p0Vect = p0Num / p0Denom
    return p0Vect, p1Vect, pAbusive

程序说明：
  首先对所有的标签进行求和，并除以总的文档长度，得到概率p(c)。因为负面的记1，正面记0，所以求得的和即是负面标签的总数。然后初始化类别概率为0。在计算每个特征的概率时，首先要对类别进行判断，当满足该类别时，对其特征进行求和，即单词在单词列表中出现的次数，因为是用’1’和’0’来标记的，所以直接求和即可，同时也需要计算总的特征数，即在类别下单词在单词列表中出现的总次数。最后计算出概率。
程序验证：

1
2
3
4
5
6
listOPosts, listClasses = loadDataSet()
myVocabList = createVocabList(listOPosts)
trainMat = []
for postinDoc in listOPosts:
    trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
p0V, p1V, pAb = trainNBO(trainMat, listClasses)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
myVocabList ['flea', 'licks', 'please', 'garbage', 'love', 'how', 'cute', 'park', 'my', 'dalmation', 'dog', 'so', 'mr', 'posting', 'stop', 'has', 'steak', 'ate', 'not', 'buying', 'help', 'maybe', 'worthless', 'quit', 'to', 'I', 'him', 'stupid', 'food', 'problems', 'take', 'is']
p0V [0.04166667 0.04166667 0.04166667 0.         0.04166667 0.04166667
 0.04166667 0.         0.125      0.04166667 0.04166667 0.04166667
 0.04166667 0.         0.04166667 0.04166667 0.04166667 0.04166667
 1.         0.         0.04166667 0.         0.         0.
 0.04166667 0.04166667 0.08333333 0.         0.         0.04166667
 0.         0.04166667]
p1V [0.         0.         0.         0.05263158 0.         0.
 1.         0.05263158 0.         0.         0.10526316 0.
 2.         0.05263158 0.05263158 0.         0.         0.
 0.05263158 0.05263158 0.         0.05263158 0.10526316 0.05263158
 0.05263158 0.         0.05263158 0.15789474 0.05263158 0.
 0.05263158 0.        ]
pAb 0.5

  例如在该数据集中，在已知的单词表中，’flea’在正面的评论中出现1次，正面评论的总特征数为24，所以概率为1/24=0.041，而在负面评论中出现0次，所以概率为0。负面评论中概率最大的单词为’stupid’，共出现3次，负面评论的总特征数为19，概率为3/19=0.15，即’stupid’是最能表征负面评论的特征。

测试算法

  对原始数据集进行贝叶斯算法训练得到其模型后，便可以根据实际的输入数据进行预测分类了。
  但现在会出现一个问题，当计算多个特征概率的乘积以获得某个类别的概率时，如果其中一个特征的概率为0，则最后的乘积也是0。为了解决这个问题，可以将所有特征出现的次数初始化为1，并将分母初始化为2。其次当多个特征的概率很小时，其乘积会越来越小，从而会影响数值的精度，为此，可以用取对数的方法，将乘积转换为求和。
训练算法程序改写为：

1
2
3
4
5
6
7
p0Num = ones(numWords)
p1Num = ones(numWords)
p0Denom = 2.0
p1Denom = 2.0
...
p1Vect = log(p1Num / p1Denom)
p0Vect = log(p0Num / p0Denom)

测试算法程序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
def classifyNB(vec2Classify, p0vec, p1Vec, pClass1):
    # 利用贝叶斯公式计算概率
    p1 = sum(vec2Classify * p1Vec) + log(pClass1)
    p0 = sum(vec2Classify * p0vec) + log(1.0 - pClass1)
    if p1 > p0:
        return 1
    else:
        return 0

def testingNB():
    listOPosts, listClasses = loadDataSet()
    myVocabList = createVocabList(listOPosts)

    trainMat = []
    for postinDoc in listOPosts:
        trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
    p0V, p1V, pAb = trainNBO(trainMat, listClasses)
    # 输入的新数据
    testEntry = {'love', 'my', 'dalmation'}
    thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
    classifyNB(thisDoc, p0V, p1V, pAb)

程序说明：
  classifyNB()函数有4个输入，待输入的新数据在特征列表中每个特征出现的次数，训练模型得到的类别0和类别1的特征概率和类别0的概率。因为是二分类，所以类别1的概率=1-类别0的概率。
  首先按照类别，将新数据的每个特征出现的次数与其类别的特征概率进行相乘相加，然后加上对应类别的概率，最后根据总的概率大小来判断分类。

三、感悟

  1. 贝叶斯算法属于有监督的预测算法，根据原始数据集训练出概率模型，然后对新的数据集进行预测。
  2. 贝叶斯算法训练的概率模型是基于贝叶斯公式的，由于数据集存在多个特征，需要对每个类别下的特征进行概率计算。
  3. 计算每个类别的特征概率时，用该类别下每个特征出现的概率除以该类别下出现的总特征个数，而不是全部类别下的总特征个数，即存在有些特征是该类别没有的。
谢谢老板！
-------------本文结束感谢您的阅读给个五星好评吧~~-------------
欢迎光临
❤️
NJTech Cxx
请多关照
❤️
❤️